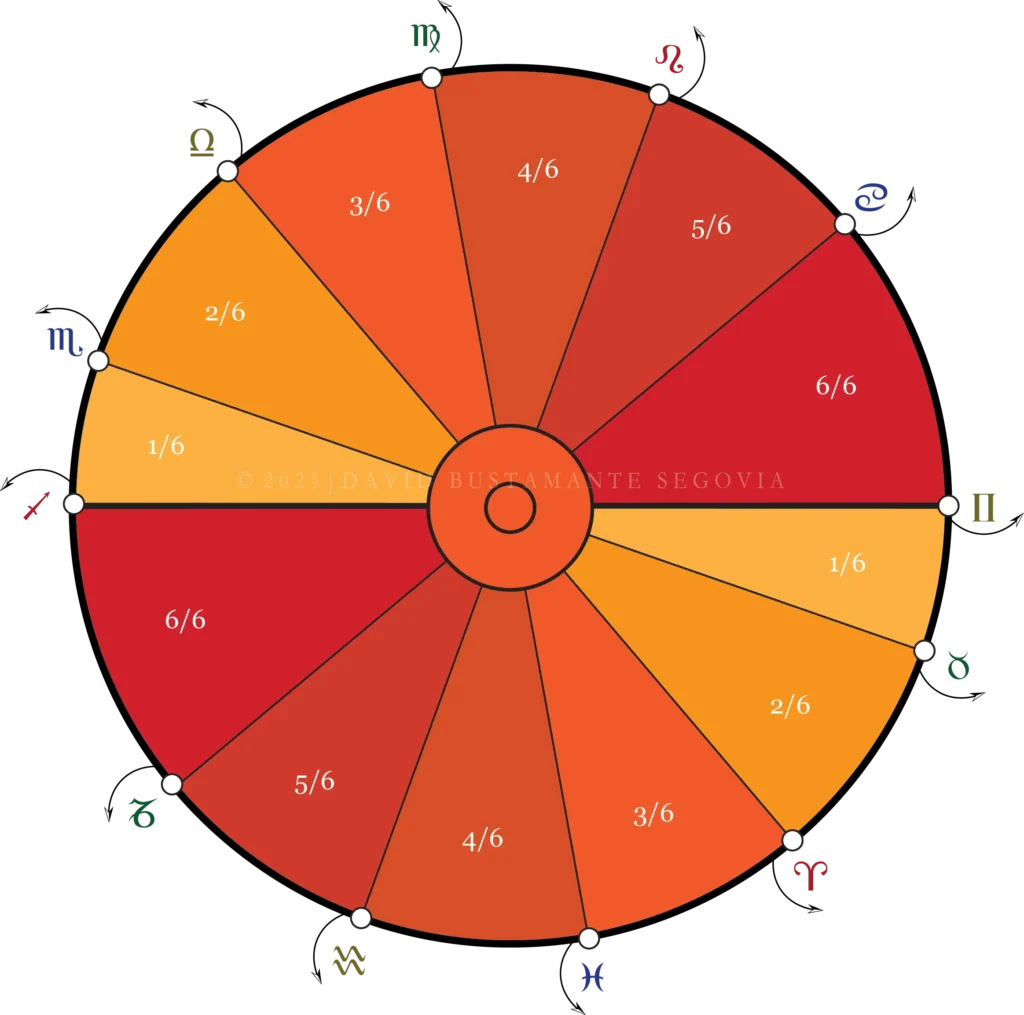
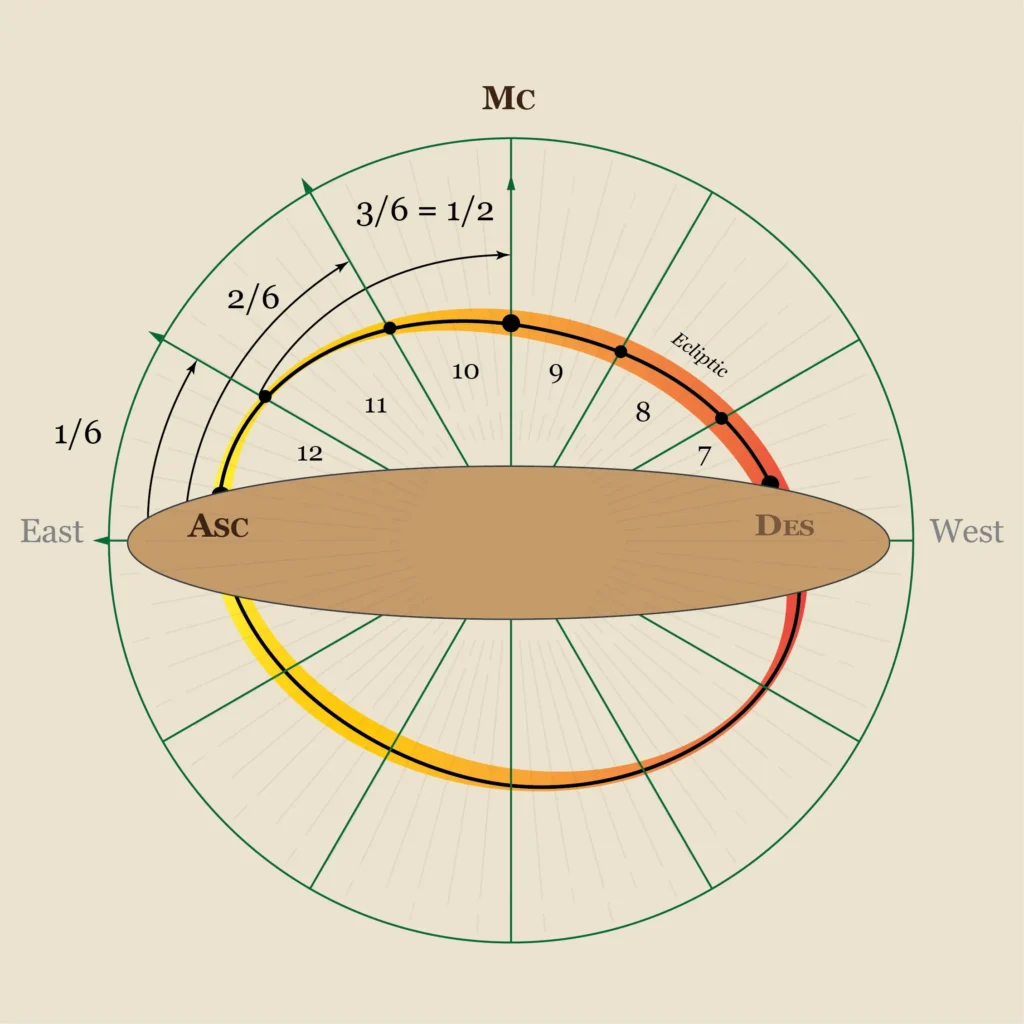
● In a Placidean measurement, each sixth of the diurnal arc (i.e. each Placidean cuspal degree) represents the path travelled by a different zodiacal degree, which bears its own clock, speed, or time of ascension. Therefore, each length of time constitutes one, two, three, four, or five sixths of the time that would have elapsed since the sun’s rise if it had occupied that degree of the ecliptic (i.e. all five cuspal degrees constitute five different trisections). When we measure the houses of an astrograph, the sun does not occupy all the degrees simultaneously, but these bear with them the time established by the sun the first time it rose or dawned with them during the year. We thus measure the time of all simultaneously and uninterruptedly in order to determine the house cusps as accurately as possible. Such measurement, however, is not trigonometric, but physical. Because the intermediate cusps constitute times at which two different ecliptic degrees will become the eleventh and twelfth house cusps, two different, additional trisections need be made, for they represent two different ascensional times. For the purposes of revealing these two degrees, however, we need find two different times of two different earlier charts whose ascending degrees would have become the relevant cusps (twelfth and eleventh, respectively) at the time of birth. Or, simply, should you prove to be awesome at triangulation, triangulate bearing in mind the ascensional times of the signs or segments of the ecliptic above the horizon at the time of birth.

● Alcabitius and Koch, for their part, are both methods of convenience only, that is, two different ways of abbreviating the Placidean exercise, so as not to bother with measuring the ascensional times of the intermediate cuspal degrees, which is why both methods assign to these a third of the amount of time of the only degree they measure: ASC, in the case of Alcabitius, and MC, in the case of Koch. In other words, under Alcabitius, the twelfth and eleventh house cusps are assigned a third (1/3) of the amount of time that the ascending degree (ASC) would have invested in travelling from the horizon to the midheaven (or one sixth 1/6 of the time that degree would have invested in travelling from the horizon to the diametrically opposite point), whereas, under Koch, the twelfth and eleventh house cusps are assigned a third (1/3) of the amount of time that the culminating degree (MC) would have invested in travelling from the horizon to the midheaven (or one sixth 1/6 of the time that degree would have invested in travelling from the horizon to the diametrically opposite point), which accounts for the displacement of the quadrant at the time of birth more conveniently than Alcabitius, for it is measuring how that quadrant or portion of the ecliptic got there at the time of birth in the first place (by placing the MC at the horizon in order to conduct the exercise, that is, in order to advance it two equal amounts of time whose thirds derive from the time of culmination of the midheaven degree only), not what the quadrant would look like after the time of birth (by placing the ASC at the midheaven in order to conduct the exercise, that is, in order to advance it two equal amounts of time whose thirds derive from the time of culmination of the ascending degree only).

● Therefore, while Koch- and Alcabitius-measured houses have the same time size, Placidus-measured houses do not (they are relative). Many confuse the proportional feature of seasonal hours (a consequence of Placidean measurement, as it is a natural, not a man-made, measurement) with the time size of a Placidean house, which is necessarily unequal.