No deje de estudiar este video en el canal de YouTube Aviation Theory

⦿ La trigonometría esférica es la herramienta según la cual el astrólogo calcula las cúspides de casas, independientemente del modelo de casas de su preferencia. Los dos métodos que mejor ilustran el uso de la trigonometría esférica son Campano (siglo trece) y Regiomontano (siglo quince), donde este último es el más elegante o newtoniano (modo correcto de dividir el espacio si tratáramos dicha dimensión como una dimensión independiente del tiempo, que no es el caso).

⦿ Cuando, no obstante, hablamos de casas naturales o ptolemaicas o ezranianas (Abraham ibn Ezra) [1], mejor conocidas según el nombre de quien popularizara dicho método (Placidus de Titis, quien completara las tablas de Giovani Antonio Magini), no tendemos a emplear trigonometría esférica alguna, sino que observamos con rigor el ritmo armónico de la bóveda celeste, es decir, el movimiento diurno o el ‘desplazamiento primario’ (del inglés ‘primary motion’), como lo haría un astrolabio de la Edad Media (véase Luís Ribeiro’s Fascinating Astrolabe). Dicho de otra manera, observaríamos con sumo rigor los tiempos ascensionales del sol en cada uno o cualquiera de los 360º de la circunferencia que llamamos eclíptica (i.e. cinturón zodiacal) en cada latitud del globo terráqueo.

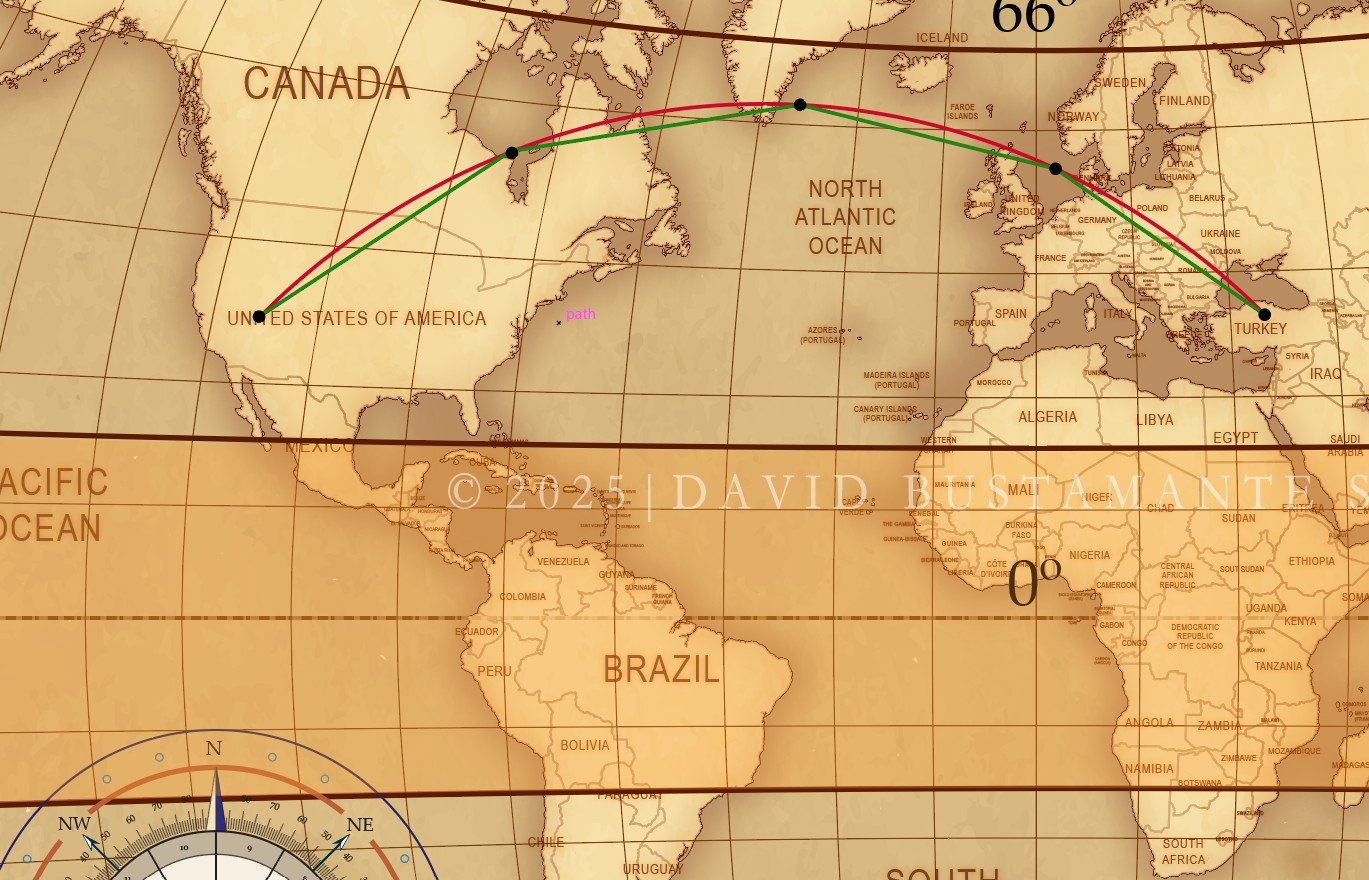
⦿ La línea roja (que, en teoría de aviación recibe el nombre de círculo máximo) representa, pues, el ejercicio de medición placidiano (natural), mientras los segmentos de líneas verdes, a su turno (que en teoría de aviación reciben el nombre de líneas rumbo), representan la expresión trigonométrica o matemática de dicho método de medición de casas, y es esta versión del sistema de casas Placidus la que la inmensa mayoría del mundo conoce o con la cual se halla familiarizada (creyendo, además, que el método es moderno o contemporáneo, en vez de el más antiguo de los métodos cuadrantes si excluyéramos las casas de Porfirio de Tiro).

⦿ Debido, no obstante, a que la versión pura del mismo se halla exenta de trigonometría esférica, es decir, debido a que no utiliza o apela al uso de los círculos máximos, no falla (porque no puede, simplemente) en ninguna región de la Tierra, incluyendo los círculos polares, mientras el resto de métodos de división de casas sí.

⦿ Es, por consiguiente, la trigonometría esférica la que falla en latitudes extremas debido a que el uso de los círculos máximos (en vez de líneas curvas u horarias, honrándose la dimensión del espaciotiempo [2] de Einstein y Minkowski) se vuelve un ejercicio obsoleto en dichas latitudes.

⦿ Descartar el plano del horizonte, a su turno, es decir, prescindir de un plano independiente al de la eclíptica o Zodiaco, no puede, por su parte, ser considerado una división de casas, sino una manera de prescindir de ellas (v. gr. casas signo, casas iguales, y, en parte, casas Porfirio). En este sentido, debo decir que fallan en cualquier latitud del globo terráqueo, si bien la mayoría no lo ve así e, incluso, se piensa que las casas iguales y las casas signo constituyen el modelo perfecto de casas por la razón que acabamos de desmentir: “Porque son modelos universales, es decir, sirven en cualquier parte de la Tierra.” Nada podría estar más lejos de la verdad, sin embargo.

⦿ Una publicación en desarrollo, Astrología polar. Sobre por qué algunos métodos de medición de casas fallan en las regiones polares, según el no enterado o el desinformado (abril de 2025), tratamos cada uno de estos puntos en detalle conjuntamente con el astrólogo británico del siglo veinte, Michael Wackford.

____________

[1] Abraham ibn Ezra se refirió al método Placidus como “el método de los tiempos ascensionales” (trad. Shlomo Sela, 2014, págs. 377, 404, 406).

[2] La curvatura del espaciotiempo no es puramente esférica, pues se describe mediante geometrías más complejas que van más allá del alcance de la trigonometría esférica. Entre ellas, la geodesia y la geometría de Riemann.