Learn the reason for which it is said that certain Zodiacal degrees never rise within the polar regions.
Be sure to check this video out on the YouTube channel Aviation Theory
⦿ Spherical trigonometry is the tool according to which the astrologer calculates the cusps of the houses, independently of the house model of their preference. The two methods that best illustrate the use of spherical trigonometry are Campanus (thirteenth century) and Regiomontanus (fifteenth century), where the latter is the more elegant or Newtonian (correct way of dividing space if we were to treat that dimension as a dimension independent of time, which is not the case).
⦿ When we speak of natural or Ptolemaic or Ezranian houses (Abraham ibn Ezra) [1], however, better known by the name of the individual who popularised them (Placidus of Titis, having completed the tables of Giovanni Antonio Magini), we do not tend to employ spherical trigonometry. Instead, we rigorously observe the harmonious rhythm of the celestial vault, that is to say, diurnal movement or primary motion, as would be observed by a medieval astrolabe (see Luís Ribeiro’s Fascinating Astrolabe). We would observe the ascensional times of the sun with the utmost rigour at each or any of the 360° of the circumference we regard as the ecliptic (i.e. zodiacal belt) at each latitude of the globe.
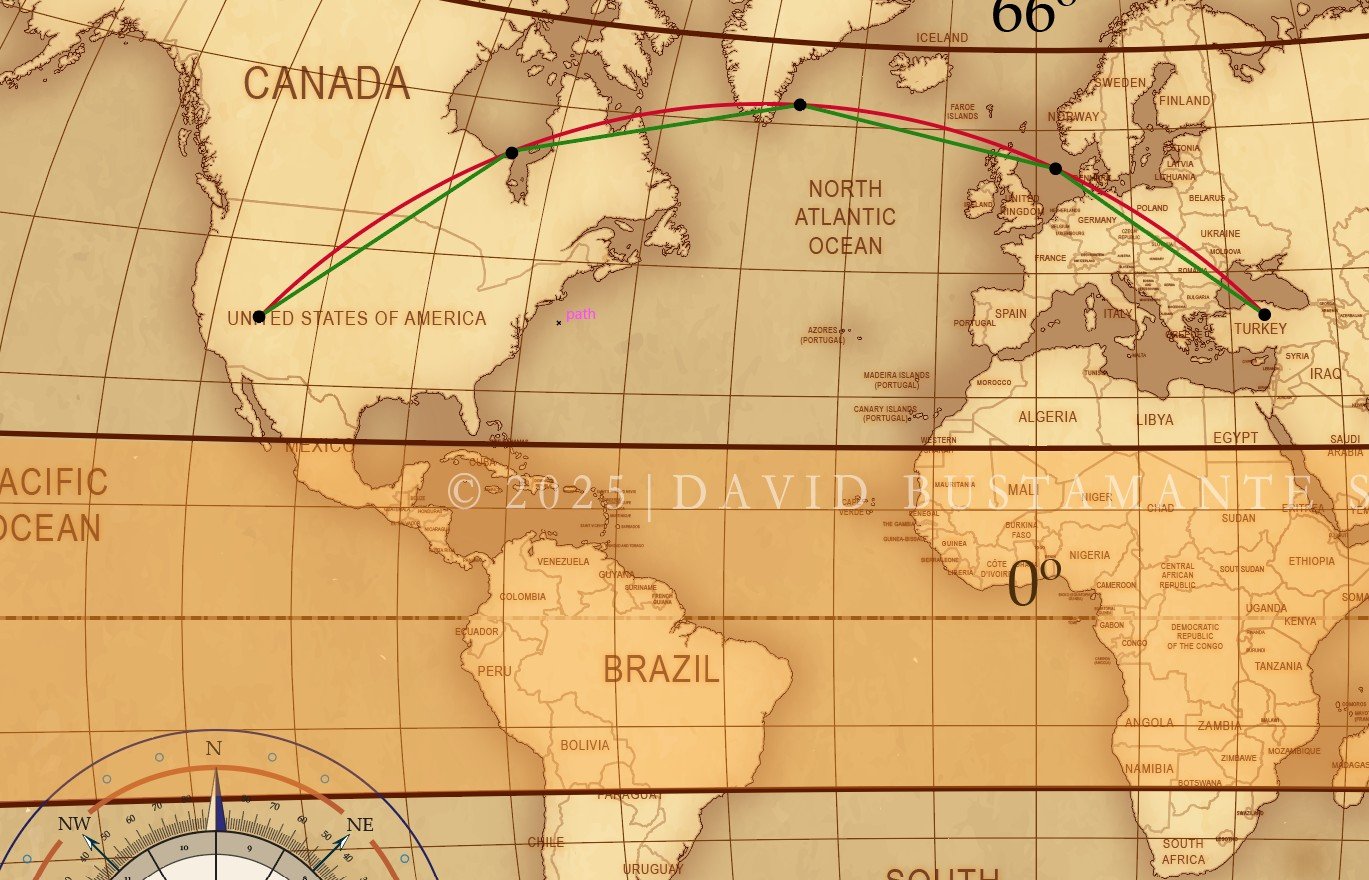
⦿ The red line (called a great circle in aviation theory) thus can be said to represent the Placidian (natural) method of house division, whereas the green line segments (called rhumb lines in aviation theory), in turn, the trigonometric or mathematical expression of said measurement of astrographic regions, and it is this version of the Placidus system of houses that the vast majority of the world knows or is familiar with (believing, moreover, that the method is modern or contemporary, rather than the oldest of the quadrant methods of house division if we were to exclude the houses of Porphyry of Tyre).
⦿ Because, however, the pure version of it is free of spherical trigonometry, that is, because it does not appeal to the use of great circles, it does not fail (because it simply cannot) in any region of the Earth, including the polar circles, whereas all other methods of house division do.
⦿ It is, therefore, spherical trigonometry that fails at extreme latitudes, as the use of great circles (instead of curved or hour lines, honouring thereby Einstein’s and Minkowski’s spacetime [2]) becomes an obsolete exercise at said latitudes.
⦿ To discard the horizon plane, in turn, that is, to dispense with a plane independent of that of the ecliptic or Zodiac, cannot, for its part, be considered a division of houses, but a way of dispensing with them (e.g. sign-houses, equal houses, and, in part, Porphyry houses). Therefore, I must say that they fail at any latitude of the globe, although most would not see it this way, even going as far as to think that equal houses and sign-houses constitute the perfect model of houses for the very reason that we have just impugned: “Because they are universal models, that is to say, they work every or anywhere on Earth.” Nothing could be further from the truth, however.
⦿ A publication under development, Polar Astrology. On why some methods of house division fail in the polar regions, according to the unaware or uninformed (April 2025), discusses each of these points in detail in conjunction with twentieth-century British astrologer Michael Wackford.
__________
[1] Abraham ibn Ezra referred to the Placidus method as “the method of the rising times” (trans. Shlomo Sela, 2014, pp. 377, 404, 406).
[2] The curvature of spacetime is not purely spherical and appears described by more complex geometries that go beyond the scope of spherical trigonometry. Among them, geodesics and Riemannian geometry.